#数楽 準素イデアルの定義がピンと来てない人をどこかで見たような気がするのでちょっとその話。Qは可換環Aの真のイデアルであるとします。「a,b∈Aかつab∈Qかつnot a∈Qならばある自然数n>0でb^n∈Qとなるものが存在する」とき、QはAの準素イデアルであると言います。続く
#数楽 続き。たぶんこの定義そのものだけを忠実に理解しようとしてピンと来なくなっている。同じ問題はもっと易しい素イデアルや極大イデアルの定義について教えているときにもよく出会います。イデアルについている形容詞の定義を理解するためには、そのイデアルで割ってできる剰余環について〜続く
#数楽 続き〜、考えてみるとよいです。同じことですが、零イデアルがその性質を満たしているのはどういうときかについて考えてみるとよいです。Iは可換環Aの真のイデアルとします。A/Iが体、整域、「その零因子はすべて冪零」であることのそれぞれとIが極大、素、準素であることは同値。続く
#数楽 続き。個人的には教育現場では最初からそれを極大、素、準素イデアルの定義に採用したいくらい。環の準同型定理の具体例での使い方を知っていれば、剰余環を計算して極大、素、準素イデアルであることを判定してもらうことも気軽にできるし。こういう易しい話も需要がありそうな感じ。
#数楽 体、整域、準素環(零因子がすべて冪零な環、primary ring)に対応する幾何がどういう感じのものなのか知っているとさらによい。あと冪零元は「無限小」だとか。「εは0ではないが、n乗すると0になってしまうくらい微小だ」というようなことも考える。
#数楽 「aの7乗しなければ0にならないが、bの6乗は0なので、aよりもbの方が『微小』である」とか。たとえば、Z/128Zにおいて(0⇔128で割り切れる)、14は7乗しなければ0にならないが、12の4乗は0になる。Z/128Zにおいて14よりも12の方が「微小」。
#数楽 続き。この話における128=2^7の7を無限に大きくする極限を考えれば、2の大きなべきで割り切れるほど「微小」となる「2進整数環」の世界が得られわけです。2を別の数に変えてもよい。個人的には無限小の直観があった方がp進数入門が楽になると思う。
#数楽 超大脱線。体や整域の定義の中に「零環でない」という条件を忘れずに含めている代数学入門書は注意深く書かれています。その条件は「素数に1を含めない」ことの一般化なので要注意なのですが、数学に強くなると細かい部分はどうにでもなるので書くのを忘れるようになる。
#数楽 あと剰余環の定義についても教科書に書いてある定義のみを忠実に理解しようとしてはまるパターンもよく見かける感じがします。(似たようなはまり方を多様体の定義でも見かけたことがある。) 剰余環Z/12Zは有理整数環Zの中で12を0とみなしてできる環であるとかを知らないと困る。
#数楽 続き。M/Nで「Mの中でNの元をすべて0とみなしてできるもの」を意味することがよくある。この「〜とみなしてできるもの」という曖昧な言い方を避けると教科書に書いてあるような定義になる。教科書的定義を出発点にするのではなく、「定義を自分で出す」という発想が大事。続く
#数楽 易しい話の続き。数学科学部レベルの代数を習ったら、中高で習った「方程式」の定義について考えてみるとよいかも。例えば勝手に剰余環R=Z[x]/(x^2-2)Z[x]を「方程式x^2=2」と呼ぶと定義してよい。任意の環Aにおける方程式x^2=2の解全体は〜続く
#数楽 続き〜、剰余環R=Z[x]/(x^2-2)Z[x]から環Aへの環の準同型写像φ全体と一対一に対応しています(α=φ(x)が解になる)。中学校レベルの方程式x^2=2とその解を環と環の準同型の言葉で完全に定式化できたわけです。続く
#数楽 x^2+y^2=1のような図形の定義になっている方程式も剰余環R=Z[x,y]/(x^2+x^2-1)Z[x,y]として定式化できる。方程式x^2+y^2=1の実数解全体はRから実数体への環の準同型写像全体と一対一に対応している。これで円の方程式も環論で扱える。
#数楽 で、環論のよくある演習問題に「Kが実数体の部分体であるときK[x,y]/(x^2+y^2-1)K[x,y]は整域だがUFDではないことを示せ」があります。Kが複素数体ならUFDになることは易しい(Laurent多項式環に同型になる)。単位円の方程式への新たな出会い。
#数楽 超易しい話という文脈では1つ前のツイートの問題は難しい方に分類されます。UFDでない例としてはK[x,y]/(y^2-x^3)K[x,y]≅K[t^2,t^3] (x=t^2, y=t^3)の方がずっと易しい。これはカスプy^2=x^3の特異点解消の例でもある。
#数楽 x=t^2, y=t^3は「x=f(t), y=g(t)の軌跡を考える。f(t)もg(t)も滑らかな函数なのに軌跡は滑らかではない例を挙げよ」の例になっています。 http://www.wolframalpha.com/input/?i=x=t**2, y=t**3 …y^2=x^3は退化した楕円曲線の例にもなっている。
#数楽 http://www.wolframalpha.com/input/?i=parametric plot x=t**2, y=t**3, z=t …parametric plot x=t**2, y=t**3, z=txyz空間内の曲線としてこれは滑らかだが、xy平面に射影すると尖がる。
#数楽 以上の例は多くの教科書でよく見かけるものです。教科書的例はやはり重要で知らないと様々な場面で理解に困ることが多い。具体的な例も一般的な概念もどちらも大事。具体例にはどの一般論に関係あるかを必ず要求し、一般論では具体例を必ず要求する。答えに詰まる人は大して理解していない。
#数楽 でも見栄をはって完璧に理解するまで誰にも話さないのは楽しみのかなりの部分を失うと思う。まだよくわかっていないことを説明しているうちに理解がすすむ方が普通だと思う。だから理解していないことの説明を聞いてくれる友人は貴重。単に聞いてもらうだけでありがたい。
#数楽 M/Nの話で代数方程式だけではなく、線形微分方程式も定式化できる。ただし非可換環が必要。正準交換関係x∂-∂x=1で定義される常微分作用素環論D=C[x,∂]を考える(∂=d/dx)。常微分方程式(∂^2+1)u=u''+1=0をD加群で定式化するには〜続く
#数楽 続き〜、ランク1の自由D加群Duの剰余加群M=Du/D(∂^2+1)u=(Duの中で(∂^2+1)u=0とみなしてできる左D加群)を考えます。これが微分方程式u''+1=0のD加群としての定式化。Dが作用している任意の函数空間Fにおけるu''+1=0の解と〜続き
#数楽 続き〜、MからFへのD加群準同型φは一対一に対応している(φ(u)が解になる)。たとえば、F=C^∞(R)の場合:φ(u)=e^{±ix}, cos x, sin xを満たすD加群準同型φ:M→C^∞(R)が一意に存在する。これで線形微分方程式も剰余加群で定式化できた。
#数楽 一般に微分作用素P∈Dについての微分方程式Pu=0はD加群M=Du/DPu=(Duの中でPu=0とみなしてできる左D加群)として定式化できます。NからD加群FへのD加群準同型全体の集合はHom_D(M,F)と書かれます。Fが具体的な函数空間ならこれはPu=0の解空間。
#数楽 https://twitter.com/genkuroki/status/778564201811841024 …訂正NじゃなくてMです。自明な誤り。まあとにかく、中学校から大学にかけて習う方程式たちは、環や加群として定式化でき、解と具体的な環や加群への準同型は一対一に対応しているということです。
#数楽 線形微分方程式をこのように定式化することの御利益はホモロジー代数を使えることです。すなわちPu=0の解空間のHom_D(M,F)だけではなく、Ext^i_D(M,D)も使える。先の例ではMの自由分解0←M←Du←DPu←0でExtを計算できます。続く
#数楽 続き。実際に計算すると、Ext^0_D(M,F)≅Hom_D(M,F)≅Ker(P:F→F)=(Pu=0のFでの解空間)Ext^1_D(M,F)≅Coker(P:F→F)=F/PF=(Pu=fの解がF内に存在しないf∈Fがどれくらいあるか)となります。
#数楽 続き。たとえばP=x=(函数xをかける作用素)でF=C[x]のとき、xu=0の解空間は自明にHom_D(M,F)=0となり、Ext^1_D(M,F)≅C[x]/xC[x]≅Cとなります。この例は基本的。デルタδ函数はxδ(x)=0をみたしているのでxu=0の解。
#数楽 よくわからない何かは「方程式」とみなせ、そこから具体的な何かへの「射」は「方程式の解」とみなせるという話は単なる再定式化ではなく数学的に意味のある形でうまく行っているということです。
#数楽 https://twitter.com/genkuroki/status/778557195273187329 …訂正:∂=d/dxに関して、x∂-∂x=1ではなく、∂x-x∂=1が正しい。これも自明な誤り。
#数楽 https://twitter.com/genkuroki/status/778486341361205248 …準素(prinary)イデアルの定義がピンと来ない人をどこかで見かけたような気がするという話から、方程式の概念を環や加群で定式化する話に脱線したのでした。その話の続き。必要な脱線であったことがわかるようにしたい。
#数楽 復習1:可換環Aの真のイデアルIが準素(primary)であるとは剰余環A/Iのすべての零因子が冪零になることであった。だから準素イデアルの概念を理解するためには零でない剰余環でその零因子がすべて冪零になるようなものについて理解すれば良さそうだ。
#数楽 復習2:有理整数環をZと書く。中学校で習う方程式x^2=2は剰余環R=Z[x]/(x^2-2)Z[x]=(Z[x]の中でx^2=2とみなしてできる環)として定式化できる。可換環Aにおけるx^2=2の解はRからAへの環準同型φと一対一に対応している(φ(x)が解になる)。
#数楽 ここから新しい話。素イデアルとはそれで割ってできる剰余環が整域になるようなイデアルのことであった。I=(x^2-2)Z[x]はZ[x]の素イデアルである。証明は環の準同型定理を使って、Z[x]/IがZ[√2]={f(√2)|f∈Z[x]}に同型であることを示せばよい。
#数楽 中学校では重解を持つ方程式x^2-2x+1=0についても習う。その方程式とx-1=0の実数解の集合は一致している。実数解の集合で重解を持つ方程式とそうでない方程式を区別することは不可能である。しかし、方程式を剰余環として定式化すればそれらを区別できる。続く
#数楽 続き。x^2-2x+1=0は剰余環R_2=Z[x]/I_2、I_2=(x^2-2x+1)Z[x]として、x-1=0は剰余環R_1=Z[x]/I_1、I_1=(x-1)Z[x]として定式化できる。環の準同型定理によって、R_1はZ[1]=Zと同型になり、続く
#数楽 続き〜、R_2はランク2の自由Z加群Z+Zεにε^2=0というルールで可換環の構造を入れたもの(Z[ε] with ε^2=0)に同型なことがわかる(x-1にεを対応させる)。
#数楽 環の準同型定理を使えない人は次のように考えてもよい。R_1の定義はZ[x]/(x-1)Z[x]で、それはZ[x]の中でx-1=0すなわちx=1とみなしてできる環のことなので、xが1で置き換えられて、R_1≅Zとなる。続く
#数楽 続き。R_2の定義はZ[x]/(x^2-2x+1)Z[x]=Z[x]/(x-1)^2Z[x]で、それはZ[x]の中で(x-1)^2=0とみなしてできる環なので、x-1が2乗すると0になる無限小量εに置き換えられて、R_2≅Z[ε] with ε^2=0となる。
#数楽 重根を持つ方程式(x-1)^2=0を環論的に定式化するときには、xを1+ε (ここでεは2乗すると0になる無限小量)で置き換えるという操作をするわけです。単根と重根の違いは冪零元(無限小量の一種)の有無で区別されます。
#数楽 で、以上に出て来た重根を表現するイデアルI_2=(x-1)^2Z[x]がZ[x]の準素イデアルになっていることもわかります。準素イデアルの話は中学校のときに習った重根の話の一般化になっているわけ。数学科の学部レベルでの代数は義務教育レベルの話をやり直している感じ。
#数楽 冪零元εは「それ自体は0ではないがそのある冪が0になるほど微小な無限小量の一種」とみなせます。このようなスタイルによって純代数的に無限小量を扱えるわけです。それによって純代数的に解析学(逐次近似が重要)の真似事ができる。冪零元を排除しないことは結構大事。
#数楽 残念なことに、大学の数学科の先生の中には、「高校以下の数学と大学数学科での数学は違う」と強調し過ぎて、学生が数学を「普通に」理解する道から離れてしまう原因を作っている人達がいるように思えます。実際には高校以下の数学と数学科での数学は内容的にダイレクトに繋がっています。
#数楽 内容的に高度になっているという違いは確かにあるのですが、同じ数学。本質的に変わったと感じる人は高校以下の数学を正しく理解していなかっただけなのだと思う。そこには運で決まっている部分が膨大にある。運の良さを奢ることなく、運の悪さに負けることなく楽しみたいものだと思います。
#数楽 primary idealの超易しい話に結構需要があったようなので続き。以下、可換環Aのf_1,…,f_r∈Aで生成されるイデアルを(f_1,…,f_r)=f_1 A+…+f_r A と書きます。この書き方は文脈による判断を要求するので要注意。続く
#数楽 続き。さらに以下、簡単のため複素数体C上で考える。k重根を持つ方程式(x-1)^k=0は剰余環R_k=C[x]/((x-1)^k)=(多項式環C[x]の中で(x-1)^k=0とみなしてできる環)=(複素数体に丁度乗すると0になる元εを付け加えてできる環)に対応します。続く
#数楽 続き。C[x]のイデアル((x-1)^k)=(x-1)^k C[x]は準素イデアルの簡単な例になっています。その準素イデアルはk乗根を持つ方程式 (x-1)^k=0 を表現している。方程式(x-1)^k=0のCでの解はkによらずに一点x=1になるのですが、~続く
#数楽 続き~、k乗根としての点x=1と単根としてのx=1を区別したくなったらどうするか。その答えの一つが「環R_k=C[x]/((x-1)^k)を考える」です。環R_kにはx-1に対応する「丁度k乗で0になる元ε」(無限小元の一種)が含まれており、~続く
#数楽 続き~、環R_k=C[x]/((x-1)^k)="C[ε] with ε^k=0" は方程式(x-1)^k=0の解の中には点x=1から無限小だけ離れた所も含まれていることを表現しています。方程式(x-1)^k=0の解は完全な1点より少し膨らんだ「点」になっている。続く
#数楽 続き。方程式(x-1)^k=0(すなわち可換環R_k=C[x]/((x-1)^k))で定義される「点」をk重点と呼ぶことにしましょう。k<lのとき、k重点よりもl重点の方が少し膨らんだ「点」になっている。自分なりに図を描いて見ると楽しいかも。直観的には中学校レベル。続く
#数楽 k重の点と同様にして、k重の直線も考えることができます。xy平面において(x-1)^k=0のような方程式で定義される「直線」をk重直線と呼ぶことにすればよい。そのときに使う可換環はC[x,y]/((x-1)^k)です。変数の個数が増えただけで先の話と何も変わらない。続く
#数楽 続き。C[x,y]のイデアル((x-1)^k)も準素イデアル。準素イデアルの定義を知ったら、以上で説明した直観的には中学校レベルの話を延々と考えてみることが必要です。「例を3つ以上考えなさい」という伝統的なアドバイスは「こういうことを勝手にやっておいてね」という意味。
#数楽 続き。1重直線(普通の直線)と2重直線の交わりはどのような「点」になるでしょうか?1重直線としてx=0 (y軸)を考え、2重直線としてy^2=0 (2重のx軸)を考えましょう。それらはC[x,y]のイデアル(x)と(y^2)にそれぞれ対応しています。続く
#数楽 続き。方程式f=g=0を表現する可換環Aのイデアルは(f,g)=fA+gAです。だから、y軸(x=0)と2重のx軸(y^2=0)の交わり(x=y^2=0)を表現するC[x,y]のイデアルは(x,y^2)=xC[x,y]+y^2C[x,y]になります。続く
#数楽 続き。代数方程式で定義された図形の幾何学的様子はその代数方程式に対応するイデアルによる剰余環で表現されているのでした。だからy軸と2重のx軸の交わりの様子は剰余環C[x,y]/(x,y^2)の構造を調べればわかる。続く
#数楽 一般に可換環Aとそのイデアル(f,g)について、A/(f,g)=(Aの中でf=g=0とみなしてできる環)だったので、C[x,y]/(x,y^2)=(C[x,y]の中でx=y^2=0とみなしてできる環)=(C[y]の中でy^2=0とみなしてできる環)=C[y]/(y^2).
#数楽 続き。C[x,y]でx=0とみなすとxが消えてC[y]になり、さらにy^2=0とみなすとC[y]/(y^2)="C[ε] with ε^2=0"になります。ゆえに、1重のy軸と2重のx軸の交わりは2重点である。そして2重になっているのは縦方向(y方向)です。続く
#数楽 続き。以上は点と直線という義務教育レベル以下の数学的対象をほんの少し一般化してみる話。(義務教育レベル以下であることを強調するためには、複素数体Cを実数体Rにしておいた方が良かったかも。) k重点とk重直線について健全な直観があればどれも「明らか」だと感じられる話。続く
#数楽 続き。k重のy軸(x^k=0)とl重のx軸(y^l=0)の交わりに対応する環はC[x,y]/(x^k,y^l)="C[ε,δ] with ε^k=0 and δ^l=0" となり、「x方向にk重にy方向にl重に膨らんでいる点」だと解釈されます。
#数楽 続き。C[x,y]のイデアル(x^k,y^l)も準素イデアル(暗黙のうちにk,l>0としていた)。もう少しややこしい例を考えれば準素イデアル分解の簡単な例も作れます。続く
#数楽 続き。C[x,y]のイデアルI=(x^2 y,x^2(x-1)^2)を考える。x^2 y=0は2重y軸と1重x軸の合併。x^2(x-1)^2=0は2重y軸と2重直線(x-1)^2=0の合併。それらの交わりは2重y軸x^2=0と2重点(x-1)^2=y=0の合併。続く
#数楽 続き。イデアルI=(x^2 y, x^2(x-1)^2)について、I=(x^2)∩((x-1)^2,y)を証明できる。(x^2)と((x-1)^2,y)はC[x,y]の準素イデアルで、I=(x^2)∩((x-1)^2,y)はイデアルIの準素分解になっている。続く

#数楽 続き。私がずっとお世話になっている無料の数式処理ソフトはSingularです。準素イデアル分解もしてくれるので、環論の勉強に使うと便利だと思います→ https://www.singular.uni-kl.de/Manual/4-0-2/sing_866.htm …pic.twitter.com/BysUDjWSbB

#数楽 続き。 pic.twitter.com/BysUDjWSbB数式処理ソフトSingularR=Q[x,y]I=(x^2y, x^2(x-1)^2)Iの準素分解は(x2)∩(y,x2-2x+1) ←(x2はxの二乗の意味)対応する素イデアルは(x)と(y,x-1)
#数楽 https://www.singular.uni-kl.de/index.php 私が個人的に数式処理ソフトのSingularをよく使っていた理由は無料でかつ量子群的な非可換環も容易に定義して扱えるからです。
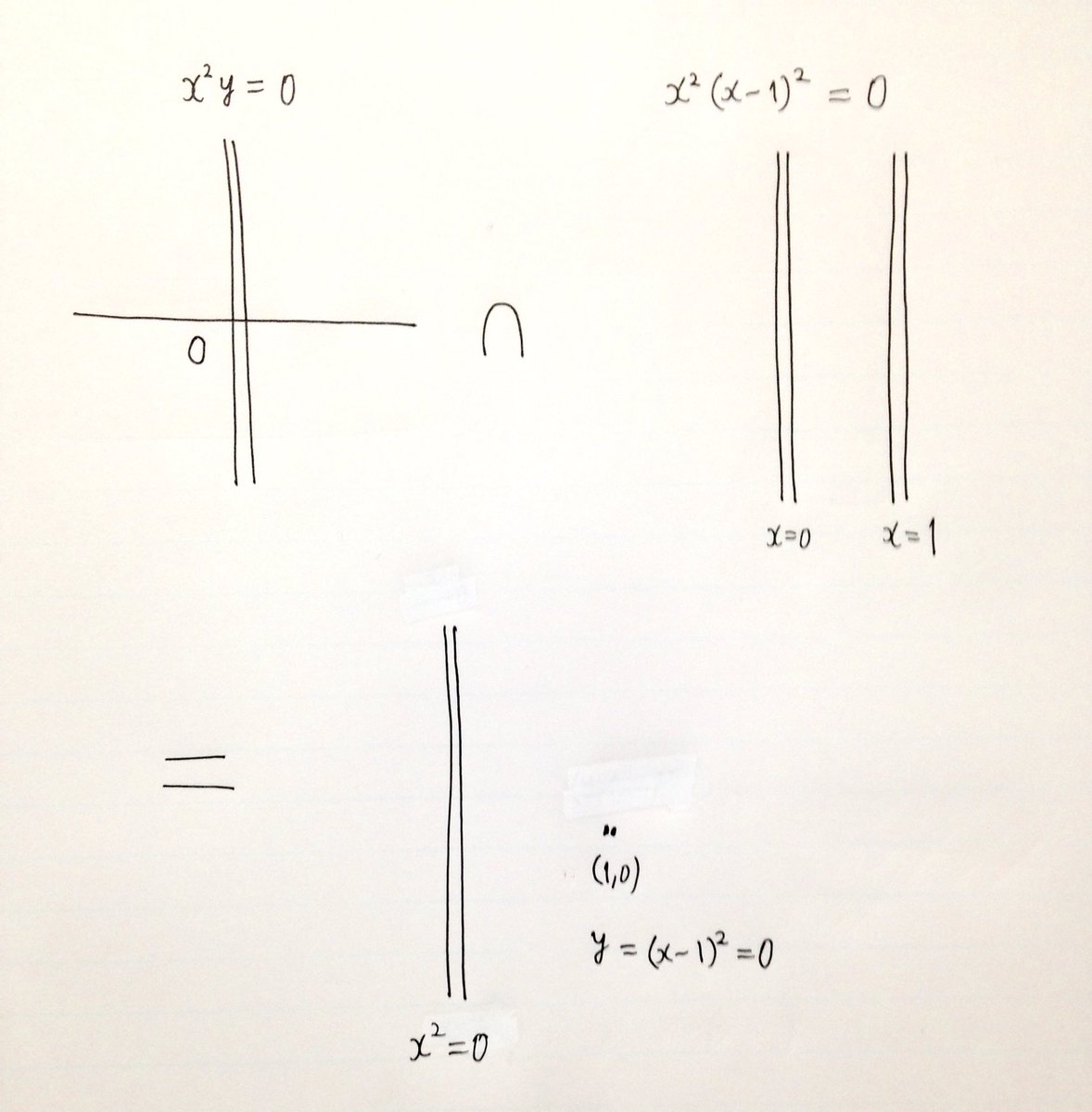
#数楽 数式処理ソフトを便利に使っているだけではなく、昔からみんなやっている「絵を描きながら考える」というのを常にやっています。イデアル(x^2y,x^2(x-1)^2)については添付画像のように描ける。pic.twitter.com/y7ueuwyXyM
#数楽 最終的に理解に達するためには「何をやってもよい」というのが基本なのに「ほとんど何もしない」から理解できなくなっていることが多いように思えます。妙な先入観のせいでやれるはずのことを選択肢から外してしまっていると苦しくなるのは当然だと思う。
#数楽 最も強力な方法は他人の頭を使って考えること。自分の頭で理解できないなら、他人の頭を利用するしかない。実は話を聞いてもらうだけで理解がすすむことが多い。数学のような分野の話を聞いてくれる人はものすごく貴重。友人の数学の単位が危なくなっていたら自分のために助けてあげるべき。
#数楽 例の追加。xy平面でx軸と放物線y=x^2は原点で接するのですが、x軸と放物線y=x^2の共通部分は単なる1点よりも「大きい」はずだと感じていた人は、以上の方法で共通部分の性質を環の言葉で表現してみるとよいと思います。
#数楽 続き。たとえば実数体R上で考えて、R[x,y]/(y,x^2-y)について考える。R[x,y]のイデアル(y,x^2-y)は方程式y=x^2-y=0に対応している。答えは次のツイートで。
#数楽 続き。R[x,y]/(y,x^2-y)=(R[x,y]の中でy=0, x^2=yとみなしてできる環)で、R[x,y]の中でy=0とみなすとyが消えてR[x]になり、さらにx^2=y=0とみなすと、R[x]/(x^2)="R[ε] with ε^2=0"となる。二重点。
#数楽 続き。二次方程式の重根だとか、y=x^2のグラフがx軸に接しているように見えるとかの話は明らかに中学校レベルです。中学生時代に感じていたはずの素朴な疑問の多くは大学で環論を学べば解消する。そして、大学で数学を勉強するときに中学校時代に描いていたような図はそのまま役に立つ。
#数楽 続き。個人的な意見では、直観的に自由に考えることができることと、論理的に正確な議論を自由にできることは強く相関している。人間は「びびり」が入ってしまうと頭がうまく働かない。いつでも論理的に厳密な安全圏に退避できる自信のある人の方が直観を自由に使い易くなると思う。
#数楽 続き。以上の説明では剰余環について「環Aの中でf=0とみなしてできる環」という言い回しを多用しましたが、そこら辺の計算はすべて環の準同型定理を使えば正当化できます。環の準同型定理を具体的にどう使えば剰余環の計算ができるかをマスターしておくとその後の勉強が超楽になるはず。
#数楽 続き。日本語の代数入門系の教科書では準素イデアルや準素イデアル分解について十分に例を挙げずに解説を終えているものがとても多いという印象があります。それじゃあ、理解が不十分なまま終わってしまう読者が続出すると思う。十分な量の例が載っていない数学の本は要注意。
線形代数の続きなら、堀田良之著『加群十話』が読み易いです。読み易くはないですが、具体例と演習問題が多い入門書としてはこれとか→ https://www.amazon.co.jp/gp/aw/d/4254114982/ … #数楽
どの教科書が自分に合うかはそれを読む本人以外に分からないことなので、数学の本がたくさんある図書館や本屋などで色々チェックしてみた方がよいと思います。「習うより慣れろ」という感じなので「慣れること」ができそうな本を選ぶといいと思います。 #数楽



